数字签名原理

一个完整的数字签名方案由三部分组成:密钥生成算法、签名算法和验证算法。密钥生成算法是根据系统参数为签名者生成公钥和私钥;签名算法是产生数字签名的某种算法,而验证算法是检验一个数字签名是否有效(即是否由指定实体生成)的某种算法。如无特殊说明,下文继续用 A 代表签名者,B 代表验证者。

下面给出数字签名的形式化定义:

(1)密钥生成算法

系统初始化产生签名方案的基本参数(M,S,K,Sign,Ver),其中 M 为消息空间,S 为签名空间，K 为密钥空间，包含私钥和公钥,Sign 为签名算法集合,Ver 为签名验证算法集合。用户 A 执行密钥生成算法生成自己的公私密钥$(k_1,k_2)$。

(2)签名算法

对任意的消息 $m \in M$,有$s=sign_{k_2}(m)$,且$s \in S$,那么 s 为消息的签名,将签名消息组(m,s)发送给签名验证者。

(3)验证算法

对于上述的$k_1 \in K$,有相应的签名验证算法:$ver_{k_1}:M \times S \rightarrow \lbrace True,False \rbrace,ver_{k_1} \in Ver$,且

$$
ver_{k1}(m, s) =
\begin{cases}
True & 当 s = sign_{k_2} \newline
False & 当s \neq sign_{k_2}
\end{cases}
$$

签名验证者收到(m,s)后,计算 $ver_{k_1}(m,s)$,若 $ver_{k_1}(m,s)=True$,则签名有效;否则签名无效。

对于每一个$k \in K$,签名函数$ sign*{k_2}$,和签名验证函数 $ver*{k1}$, 是容易计算的。而验证函数 $ver{k1}$是公开的,同时还要求对任意的消息 m,在未知$k_2$条件下从集合 S 中选取 s 使得 $ver{k_1}(m,s)=True$ 是非常困难的,也就是说,攻击者对消息 m 产生有效的签名 s 是不可能的。

根据定义,在进行私钥签名前,先进行消息关键信息提取。

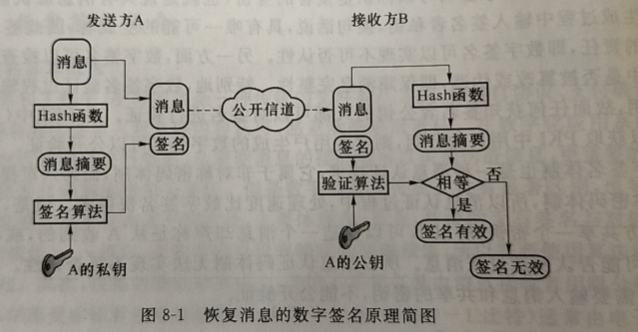
如图 8-1 所示,发送方 A 将消息用 Hash 算法产生一个消息摘要(Message Digest),这个消息摘要有两个重要特性:抗碰撞性和摘要长度固定,使得任何消息产生的签名值长度是一样的。发送方 A 产生消息摘要后,用自己的私钥对摘要进行加密,这个加密后的消息摘要就是数字签名，随后发送方 A 将消息与签名发给接收方 B。B 接收到消息及其签名后,用发送方 A 的公钥解密这个签名,获得由发送方 A 生成的消息摘要,接着用发送方 A 所用 Hash 算法重新生成所获得消息的摘要,然后比对这两个摘要。如果相同,说明这个签名是发送方 A 针对这个消息的有效签名;如果不相同,则签名无效。

1.png

依据上述数字签名的基本原理,人们设计出了众多不同种类的数字签名方案,下面将介绍常用数字签名的实现方案。

基于 RSA 的签名方案

RSA 签名方案是目前使用较多的一个签名方案,它的安全性是基于大整数因子分解的困难性。RSA 签名方案的密钥生成算法与 RSA 加密方案完全相同。关于 RSA 加密算法我也写了一篇 👉点击直达

  1. 密钥生成算法

    首先选取两个满足安全要求的大素数 p 和 q,计算 n=pq,及其欧拉函数 $\varphi(N)=(p-1)(q-1)$。然后随机选取整数$ e(1<e <\varphi(N)$,满足 $gcd(e，\varphi(N))$=1。采用如下方式计算 $d,d \equiv e^{-1}(mod \varphi(N))$,则签名者 A 的公为(n,e),私为 d。p 和 q 是秘密参数,需要保密。如不需要保存,计算出 d 后可销毁 p、q。

  2. 签名算法
    设待签名的消息为 $m \in Z_n$.,利用一个安全的 Hash 函数 h 来产生消息摘要 h(m),然后签名者 A 用下面算法计算签名$s \equiv h(m)^d(mod n)$,则 s 是消息 m 的签名。(s,m)发送给 B。

  3. 验证算法
    签名接收者 B 收到消息 m 和签名 s 后,首先,利用上述 Hash 函数 h 计算消息摘要 h(m);
    然后,检验等式$ h(m)mod n \equiv s^e(mod n)$是否成立。若成立,则签名有效;否则,签名无效。

  4. 正确性
    证明如果所有算法按步骤执行,则接收者 B 输出签名有效。

    因为

    $$
    s \equiv h(m)^d(mod \ n),de \equiv 1(mod \ \varphi(n)), \varphi(n) = (p - 1)(q - 1)
    $$

    所以

    $$
    \begin{align}
    s^e \ mod \ n &= h(m)^{ed} \ mod \ n = h(m)^{k \varphi(n) + 1} \ mod \ n = h(m)h(m)^{k \varphi(n) } \ mod \ n \newline
    &= h(m)[h(m)^{\varphi(n)}]^k \ mod \ n = h(m) \ mod \ n(其中k为整数)
    \end{align}
    $$

    注意,如果 h(m)与 n 不互素，上面等式也成立

案例

(1)密钥生成算法
假设 A 选取 p=13,q=11,e=13,则有 n=pq=143,$\varphi (n)=(p-1)(q-1)=12 \times 10=120$。求解 ed=13d=1(mod 120)得 d=37。因此 A 的公钥为(n=143,e=13);私钥为 d=37。

(2) 签名算法
假定消息 m 的 Hash 值 h(m)=16,则计算 m 签名$s=(m) ^ d \ mod \ n=16^{37} \ mod \ 143= 3$。

(3)验证算法
接收者 B 收到签名后,计算 $s^e \ mod \ n=3^{13} \ mod \ 143=16,h(m)=16 \equiv s^e \equiv 16(mod \ 143)$成立,因此,B 验证此签名有效。
注意，本例旨在说明签名方案的实现过程,为计算方便所选参数均较为简单。在目前实际应用中推荐素数长度至少为 1024 比特。

C++ 代码

因为数字签名主要的作用是验证而不是加密和解密，所以我这里用的参数比较简单，并且 hash 函数我随便写的，如果需要了解 hash 函数可以去看我写的MD5 算法和SHA1 算法.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <sstream>

#define x first
#define y second

using namespace std;

const int N = 100010;

typedef long long LL;

string clear_text; //明文
string secret_text; //密文

LL p, q;//两个安全大素数
LL e, n;//公钥
LL private_key; //私钥
LL Euler;// 欧拉函数
LL sign; // 数字签名

int res; //选择加密还是解密

LL qmi(LL a, LL k, LL p) //快速幂求余数
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}



LL exgcd(LL a, LL b, LL &x, LL &y) // 欧几里得扩展算法
{
    if(!b)
    {
        x = 1, y = 0;
        return a;
    }

    LL d, x1, y1;
    d = exgcd(b, a % b, x1, y1);
    x = y1, y = x1 - a / b * y1;

    return d;
}

string Hash(string s) // 将字符串转为string类型的数字
{
    int sum = 0;
    for(int i = 0; i < s.size(); i ++) sum += s[i];
    return to_string(sum);
}

void encrypt(string s) // 签名
{
    string ha = Hash(s); // 随便写的hash函数
    LL num = stoi(ha);
    LL k, d;
    n = p * q;
    Euler = (p - 1) * (q - 1);

    exgcd(e, Euler, d, k); // 利用欧几里得扩展算法获取私钥d
    private_key = d;
    cout << "公钥（e,n）为：(" << e << "," << n << ")" << endl <<
    "私钥d为：(" << private_key << ")" << endl;
    sign = qmi(num, d, n);
    cout << "最终发送给B的是明文hash后的值的签名s和明文m为(" << sign << "," << s << ")" <<endl;
}

void encode(LL s, string m) //解密
{
    string ha = Hash(m); // 随便写的hash函数
    LL num = stoi(ha);
    n = p * q;

    if(num % n == qmi(s, e, n))
    {
        cout <<"经过验证后签名有效" <<endl;
    } else {
        cout << "经过验证后签名无效" <<endl;
    }
}

int main()
{
    cout << "请给出两个大素数p，q和公钥e" << endl;
    cin >> p >> q >> e;

    cout << "请输入1选择签名，或者输入2选择验证" << endl;
    cin >> res;

    if(res == 1)
    {
        cout << "请输入明文" << endl;
        cin >> clear_text;
        encrypt(clear_text);
    }
    else if(res == 2)
    {
        cout << "请输入签名和明文" << endl;
        cin >> sign >> clear_text;
        encode(sign, clear_text);
    }

    return 0;
}

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//签名
请给出两个大素数p，q和公钥e
11 13 13
请输入1选择签名，或者输入2选择验证
1
请输入明文
a
公钥（e,n）为：(13,143)
私钥d为：(37)
最终发送给B的是明文hash后的值的签名s和明文m为(136,a)

// 验证（正确）
请给出两个大素数p，q和公钥e
11 13 13
请输入1选择签名，或者输入2选择验证
2
请输入签名和明文
136 a
经过验证后签名有效

// 验证（错误）
请给出两个大素数p，q和公钥e
11 13 13
请输入1选择签名，或者输入2选择验证
2
请输入签名和明文
1 a
经过验证后签名无效

安全性

从上述 RSA 签名方案中可以看到在签名时使用了 Hash 函数，这个函数的使用较之单纯对消息本身进行签名具有更好的抗攻击性。如果不使用 Hash 函数,则对消息 mm 的签名分别为 S 三 m(mod n),三 m%(mod n)。假设攻击者获得了这两个签名，就可以伪造消息 mim2 的有效签名 S1S2。这是因为,RSA 方案的这种乘特性,有时也称为同态特性,(ss)=sis 三 mm(mod n)(证明参照前面方案正确性的证明)。使用安全的 Hash 函数就可以避免类似这样的攻击，从而提高签名体制的安全性。另外,对于大消息而言,将其映射到固定长度再签名，大大提高其签名和验证的效率。

此外，RSA 签名方案还存在签名可重用的问题，即对同一消息在不同时刻签名是相同的这个问题可以通过在每次签名中引人不同随机数来解决,在后面提到的数字签名方案中对此解决方法均有所体现。