数字签名原理

一个完整的数字签名方案由三部分组成:密钥生成算法、签名算法和验证算法。密钥生成算法是根据系统参数为签名者生成公钥和私钥;签名算法是产生数字签名的某种算法,而验证算法是检验一个数字签名是否有效(即是否由指定实体生成)的某种算法。如无特殊说明,下文继续用 A 代表签名者,B 代表验证者。

下面给出数字签名的形式化定义:

(1)密钥生成算法

系统初始化产生签名方案的基本参数(M,S,K,Sign,Ver),其中 M 为消息空间,S 为签名空间，K 为密钥空间，包含私钥和公钥,Sign 为签名算法集合,Ver 为签名验证算法集合。用户 A 执行密钥生成算法生成自己的公私密钥$(k_1,k_2)$。

(2)签名算法

对任意的消息 $m \in M$,有$s=sign_{k_2}(m)$,且$s \in S$,那么 s 为消息的签名,将签名消息组(m,s)发送给签名验证者。

(3)验证算法

对于上述的$k_1 \in K$,有相应的签名验证算法:$ver_{k_1}:M \times S \rightarrow \lbrace True,False \rbrace,ver_{k_1} \in Ver$,且

$$
ver_{k1}(m, s) =
\begin{cases}
True & 当 s = sign_{k_2} \newline
False & 当s \neq sign_{k_2}
\end{cases}
$$

签名验证者收到(m,s)后,计算 $ver_{k_1}(m,s)$,若 $ver_{k_1}(m,s)=True$,则签名有效;否则签名无效。

对于每一个$k \in K$,签名函数$ sign*{k_2}$,和签名验证函数 $ver*{k1}$, 是容易计算的。而验证函数 $ver{k1}$是公开的,同时还要求对任意的消息 m,在未知$k_2$条件下从集合 S 中选取 s 使得 $ver{k_1}(m,s)=True$ 是非常困难的,也就是说,攻击者对消息 m 产生有效的签名 s 是不可能的。

根据定义,在进行私钥签名前,先进行消息关键信息提取。

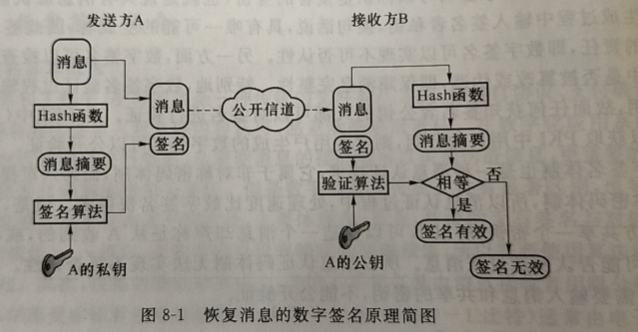
如图 8-1 所示,发送方 A 将消息用 Hash 算法产生一个消息摘要(Message Digest),这个消息摘要有两个重要特性:抗碰撞性和摘要长度固定,使得任何消息产生的签名值长度是一样的。发送方 A 产生消息摘要后,用自己的私钥对摘要进行加密,这个加密后的消息摘要就是数字签名，随后发送方 A 将消息与签名发给接收方 B。B 接收到消息及其签名后,用发送方 A 的公钥解密这个签名,获得由发送方 A 生成的消息摘要,接着用发送方 A 所用 Hash 算法重新生成所获得消息的摘要,然后比对这两个摘要。如果相同,说明这个签名是发送方 A 针对这个消息的有效签名;如果不相同,则签名无效。

1.png

依据上述数字签名的基本原理,人们设计出了众多不同种类的数字签名方案,下面将介绍常用数字签名的实现方案。

ElGamal 签名体制

T. EIGamal 于 1985 年提出了一个基于有限域离散对数问题的数字签名方案,美国 NIST 确立的数字签名标准(Digital Signature Standard,DSS)即是在它基础上修订的。EIGamal 数字签名方案是一种非确定性的签名方案,即对给定的一个消息,由于选择的随机数不同而产生不同的数字签名,并且验证算法均会判断为有效。下面简要介绍其方案的实现过程。

  1. 密钥生成算法

    选择一个满足安全性要求的大素数 p,然后选择一个生成元 $g \in Z^_p$;和随机数$x \in _RZ^_p$，,计算$y \equiv g^x(mod\ p)$。则签名者 A 的公钥为(p，g，y),私钥为 x。

  2. 签名算法
    设待签消息为 m，签名者选择随机数$k \in _RZ^*_p$;,计算:

    $$
    \begin{aligned}
    &r \equiv g^k(mod \ p) \newline
    &s \equiv [h(m)-xr]k^{-1}(mod \ (p-1))
    \end{aligned}
    $$

    则对消息 m 的数字签名为(r，s),其中 h 为安全的 Hash 函数

  3. 验证算法

    签名接收者 B 收到消息 m 和签名(r，s)后,首先计算 h(m),然后验证下列等式是否成立

    $$
    y^rr^s \equiv g^{h(m)}(mod \ p)
    $$

    如等式成立,则签名有效;否则,签名无效。

  4. 正确性

    如果所有算法按步骤执行,则接收者输出签名有效,因为

    $$
    r \equiv g^k(mod \ p), s \equiv [h(m) - xr]k ^{-1}(mod \ (p - 1))
    $$

    所以

    $$
    \begin{aligned}
    & ks \equiv h(m) - xr(mod \ (p - 1)) \newline
    & g^{ks} \equiv g^{h(m) - xr}(mod \ p) \newline
    & g^{ks}g^{xr} \equiv g^{h(m)}(mod \ p) \newline
    & y^rr^s \equiv g^{h(m)}(mod \ p)
    \end{aligned}
    $$

案例

  1. 密钥生成算法

    假设 A 选取素数 p=19,$Z^*_p$的生成元 g=2。选取私钥 x=15,计算:

    $$
    y=g^x \ mod \ p=2^{15} \ mod \ 19 = 12
    $$

    则 A 的公钥是(p=19，g=2，y=12)。

  2. 签名算法
    设消息 m 的 Hash 值 h(m)=16,则 A 选取随机数 k = 11，计算:

    $$
    \begin{aligned}
    &r=g^k \ mod \ p \equiv 2^{11} \ mod \ 19=15\newline
    &k^{-1} \ mod \ (p-1) = 5
    \end{aligned}
    $$

    最后计算签名

    $$
    s=[h(m)-xr]k^{-1} \ mod \ (p-1)=5(16-15 \times 15) \ mod \ 18=17
    $$

    A 对 m 的签名为(15，17)。

  3. 验证算法

    接收者 B 得到签名(15,17)后计算:

    $$
    \begin{aligned}
    y^rr^s \ mod \ p=12^{15}15^{17} \ mod \ 19=5\newline
    g^{h(m)} \ mod \ p \equiv 216 \ mod \ 19=5
    \end{aligned}
    $$

    验证等式

    $$
    y^rr^s \equiv g^{h(m)}(mod \ p)
    $$

    成立，因此 B 接受签名。

    注意,本例旨在说明该方案的实现过程,为计算方便所选参数均较为简单。按目前计算能力,通常使用 1024 比特或更大的模数。

C++代码

在写代码的时候我并没有学习优先于离散对数问题~~（懒）~~，因此，关于生成元 g 的知识我并不清楚，我是直接 copy 的生成元函数，但是我会适当的加上我的理解的注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
#include <stdio.h>
#include <time.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>

using namespace std;

typedef long long LL;

int mod(int a,int b){
	int ans;
	while(a<0){
		a=a+b;
	}
	ans=a%b;
	return ans;
}

// 指数运算
// 输入a和b
// 输出a的b次方
int power(int a, int b)
{
	int temp = a;
	for(int i=1 ; i<b ; i++)
	{
		temp = temp * a;
	}
	return temp;
}

// 判断一个数是否为素数
// 输入一个数a
// 返回：如果a是素数，返回true ； 否则返回false
bool Prime(int a)
{
	for(int i=2 ; i<= (a/2) ; i++)
	{
		if((a % i) == 0)
		{
			return false;
		}
	}
	return true;
}

// 辗转相除法
// 输入 a 和 b
// 返回 a和b 的最大公约数
int gcd(int a , int b)
{
    while(b!=0)
    {
        int temp = a % b;
        a = b;
        b = temp;
    }
    return a;
}

// 欧拉函数
// 输入a
// 返回a的欧拉函数值
int euler(int a)
{
	int b = 0;
	for(int i=1 ; i<a ; i++)
	{
		if(gcd(a,i) == 1)
		{
			b += 1;
		}
	}
	return b;
}

// 求阶函数
// 作用是找到最小的正整数 p（p < n），p % a == 0
int order(int a, int n, int b)
{
	int  p = 1;

	while( p<=n && power(b,p%a) != 1)
	{
		p += 1;
	}

	p = p - 1;

	if (p <= n)
	{
		return p;
	}
	else
	{
		return -1;
	}
}

// 公钥p的生成函数
int Generate_p()
{
	srand((unsigned int)time(NULL));
	int p = (rand() % (10000 - 1000 + 1) + 1000);

	for(; p<10000 ; p++)
	{
		if (Prime(p)==true)
		{
			return p;
		}
	}
}

// 公钥g的生成函数
int Generate_g(int p)
{

	int n = euler(p);

	for(int a = 2; a<p ; a++)
	{

		if(order(p,n,a) == n)
		{
			return a;
		}
	}
}

// 密钥x的生成函数
int Generate_x(int p)
{
	srand((unsigned int)time(NULL));
	int d = rand() % ( p-2-2+1) + 2;

	return d;
}

// 随机数k的生成函数
int Generate_k(int p)
{
	srand((unsigned int)time(NULL));
	int X = rand() % p;

	return X;
}
// 快速模幂运算
// 形式为 (a^b) mod c
// 输入 a 、b 和 c  因为要求a^b ， 因此是长整数
// 返回 (a^b) mod c 计算结果
int qmi(LL a, LL b, int c)
{
    int res = 1;
    while(b > 0)
    {
        if(b & 1)
        {
            res = (res * a) % c;
        }

        b = b >> 1;
        a = (a * a) % c;
    }
    return res;
}


// 求解乘法逆元
// 输入num 和 mod。 求num 在 mod 下的乘法逆元
// 返回num 在 mod 下的乘法逆元
int inverse(int num,int mod)
{
    int a = num;
    int b = mod;
    int x = 0, y = 1, x0 = 1, y0 = 0;
    int qt, temp;

	while(b != 0)
	{
		qt = a / b;
        temp = a % b;

		a = b;
        b = temp;

		temp = x; x = x0 - qt * x; x0 = temp;
        temp = y; y = y0 - qt * y; y0 = temp;
	}

    if(x0 < 0)
    {
        x0 += mod;
    }

    return x0;
}




int main()
{
    cout << "ElGamal签名验证开始O(∩_∩)O" << endl;
    cout << "=================================================" <<endl;
	//ElGamal密钥生成
	cout <<"1.ElGamal密钥生成如下:" << endl << endl;
	int p = Generate_p();
	int g = Generate_g(p);
	int x = Generate_x(p);
	int y = qmi(g, x, p);
	cout << "随机数x为:" << x << endl;
	cout << "签名者A的公钥{p,g,y}为:{" << p << "," << g << "," << y << "}" << endl;
    cout << "=================================================" <<endl;

	cout <<"2.ElGamal签名开始:" << endl << endl;
	int k = 1; // 随机数
	int in_k = inverse(k, p - 1); // k在mod(p-1)下的逆元
	int hm = Generate_p(); // 随机一个明文
	int r = qmi(g, k, p);
	int s = mod((hm - x * r) * in_k , (p - 1));
	cout << "明文hash后的值为" << hm << endl;
	cout << "随机数k和逆元in_k为:" << k << ","<< in_k <<endl;
	cout << "A对消息的数字签名{r,s}为:{" << r << "," << s << "}" << endl;
    cout << "=================================================" <<endl;

    cout <<"3.ElGamal验证开始:" << endl << endl;
    //防止计算过程中量太大，将算式拆分多次mod
    //y = 12,r = 15, p = 19, s = 17;
    //hm = 16,g = 2;
    int yr = qmi(y, r, p);
    int rs = qmi(r, s, p);
    int yrrs = mod(yr *rs, p);

    int ghm = qmi(g, hm, p);
    cout << "通过y,r,p计算yrrs mod p的值为:" << yrrs <<endl;
    cout << "通过g,hm,p计算ghm mod p的值为:" <<ghm << endl;
    if(yrrs == ghm) cout << "两值一致，数字签名验证有效!";
    else cout << "两值不一致，数字签名验证无效!";

	return 0;
}

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ElGamal签名验证开始O(∩_∩)O
=================================================
1.ElGamal密钥生成如下:

随机数x为:3998
签名者A的公钥{p,g,y}为:{4001,2,3001}
=================================================
2.ElGamal签名开始:

明文hash后的值为4001
随机数k和逆元in_k为:1,1
A对消息的数字签名{r,s}为:{2,5}
=================================================
3.ElGamal验证开始:

通过y,r,p计算yrrs mod p的值为:2
通过g,hm,p计算ghm mod p的值为:2
两值一致，数字签名验证有效!

安全性

使用 EIGamal 数字签名方案应注意以下安全问题:

  1. 随机数 k 值的选取和保管

    首先,k 值不能泄露。如果 k 值泄露,则容易计算$ x=[ h(m)-sk]r^{-1} \ mod \ (p-1$),签名者
    的私钥泄露。

    其次，随机数 k 不能重复使用。假设 k 用来对两个不同的消息签名，则 r 相同,即$(r,s_1)是m_1$的签名,$(r,s_2)是m_2$的签名。因为

    $$
    \begin{aligned}
    s_1 \equiv [h(m_1)-xr]k^{-1} \ (mod \ (p-1))\newline
    s_2 \equiv [ h(m_2)-xr]k^{-1} \ (mod \ (p-1))
    \end{aligned}
    $$

    那么有

    $$
    (s_1-s_2)k \equiv [ h(m_1)-h(m_2)](mod \ (p-1))。
    $$

    又因为消息$m_1和m_2$不同,则$s_1-s_2 \neq 0 \ mod \ (p-1)$的概率很大,则

    $$
    k \equiv h(m_1)-h(m_2)^{-1}(mod \ (p-1))
    $$

    进而容易计算签名者的私钥 x。
    最后，签名者多次签名时所选取多个 k 之间无关联。例如，三个不同的签名所选取的随机数为$ k_1、k_2、k_3$,满足条件$k_3= k_1+k_2$，显然有$r_3= r_1 r_2$,则:

    由$s \equiv [h(m)-xr]k^{-1} \ (mod \ (p-1))$可得$h(m) \equiv (ks+xr)(mod \ (p-1))$

    因此有:

    $$
    \begin{aligned}
    h(m_1)=(xr_1+ k_1s_1)(mod \ (p-1)) \newline
    h(m_2)=(xr_2+ k_2s_2)(mod \ (p-1)) \newline
    h(m_3)=(xr_3+ k_3s_3)(mod \ (p-1))
    \end{aligned}
    $$

    对以上三式分别乘以$s_2s_3,s_1s_3,s_1s_2
    $ 得:

    $$
    \begin{align}
    h(m_1)s_2s_3=(xr_1s_2s_3+ k_1s_1s_2s_3)(mod \ (p-1)) \newline
    h(m_2)s_1s_3=(xr_2s_1s_3+ k_2s_1s_2s_3)(mod \ (p-1)) \newline
    h(m_3)s_1s_2=(xr_3s_1s_2+ k_3s_1s_2s_3)(mod \ (p-1))
    \end{align}
    $$

    计算式(1)+式(2)-式(3)得

    $$
    x\equivh(m_1)s_2s_3+ h(m_2)s_1s_3- h(m_3)s_1s_2^{-1}(mod \ (p-1))
    $$

    就可以从中推出签名者的私钥 x。
    由此可见，随机数 k 的选取和保管对私钥 x 的保密性起着重要的作用。此外，随机数的使用也保证了签名方案的不可重用性，这是因为在不同时刻选取的随机数不同，即使对同一消息进行签名，也会产生不同的结果,因而避免了 RSA 签名出现的签名重用问题。

  2. Hash 函数的应用
    如果未使用 Hash 函数则签名方案容易受到攻击。例如攻击者可以选取任一整数对(u,v),满足 gcd(u,p-1)=1。计算$r=g^uy^v \ (mod \ p)，s \equiv -rv^{-1}(mod \ (p-1))和m \equiv su(mod \ p)$,则消息 m 及其签名(r,s)可以被验证者接受,即攻击者成功进行存在性伪造。这是因为
    $$
    y^rr^s \equiv y^r(g^ug^v)^s \equiv y^{r + sv}·g^{us} \equiv y^{r+(-rv^{-1})}·g^{su} \equiv g^m(mod \ p)
    $$
    又因为$g^m \equiv g^{su}(mod \ p)$也就是说,签名(r,s)使等式$y^rr^s \equiv g^m(mod \ p)$成立。可见,使用 Hash 函数能够有效地提高 EIGamal 数字签名方案的安全性。