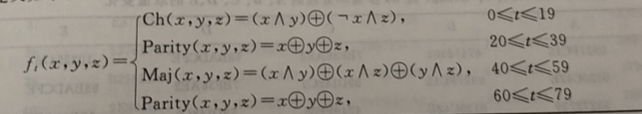Hash 函数结构

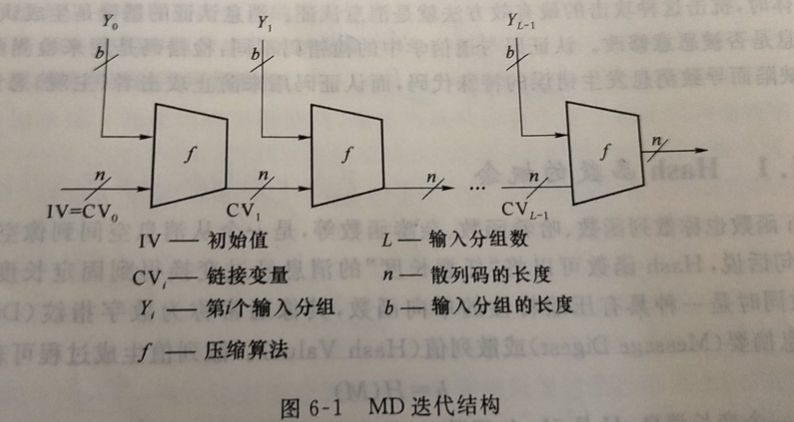
Hash 函数的一般结构如图6-1所示,称为Hash 函数迭代结构，也称为MD 结构。它由 Merkle 和 Damgard 分别独立提出,包括 MD5,SHA1 等目前所广泛使用的大多数 Hash 函数都采用这种结构。MD 结构将输人消息分为L个固定长度的分组,每一分组长为b位,最后一个分组包含输入消息的总长度,若最后一个分组不足b位时,需要将其填充为b位。由于输人包含消息的长度,所以攻击者必须找出具有相同散列值且长度相等的两条消息,或者找出两条长度不等但加入消息长度后散列值相同的消息,从而增加了攻击的难度。

1.png

迭代结构包含一个压缩函数f。压缩函数f有两个输入:一个是前一次迭代的n 位输出,称为链接变量;另一个是消息的b位分组，并产生一个 n 位的输出。因为一般来说消息分组长度b大于输出长度n,因此称之为压缩函数。第一次迭代输入的链接变量又称为初值变量,由具体算法指定,最后一次迭代的输出即为散列值。

SHA1 算法

1993 年美国国家标准技术研究所 NIST 公布了安全散列算法 SHA0(Secure Hash Algrithm)标准,1995 年 4 月 17 日公布的修改版本称为 SHA1,SHA1 在设计方面大程度上是仿 MD5 的但它对“任意”长度的消息生成 160 比特的消息摘要(MD5 仅仅生成 128 位的),因此抗穷举搜索能力更强。它有 5 个参与运算的 32 位寄存器字，消息分组和填充方式与 MD5 相同,主循环也同样是 4 轮,但每轮进行 20 次操作,包含非线性运算、移位和加法运算非线性函数、加法常数和循环左移操作的设计与 MD5 有一些区别。

说实话和 MD5 大差不差，有兴趣可以先去看我之前写的MD5 算法,看完 MD5 再看 SHA1 应该就没什么问题

1.SHA1 原理

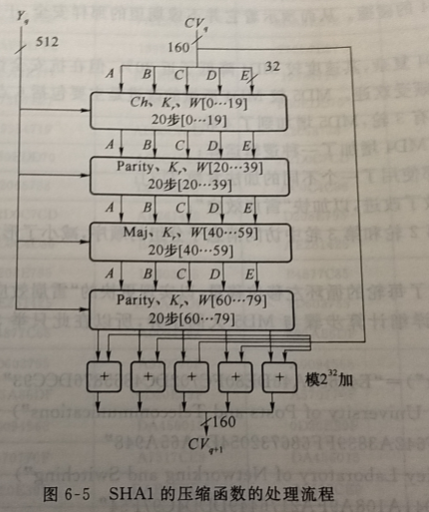
SHA1 算法的输人是最大长度小于$ 2^{64}$比特的消息,输人消息以512 比特的分组为单位处理,输出是 160比特的消息摘要。图 6-5 显示了处理消息输出消息摘要的整个过程，该过程包含下述步骤。

1.png

1.附加填充位

在长度为 K bits 的原始消息数据尾部填充长度为P bits的标识100…0，$1 \leq P \leq 512 $(即至少要填充1个bit)，使得填充后的消息位数为：$K + P \equiv 448 (mod 512).$然后在消息后附加64 比特的无符号整数，其值为原始消息的长度。产生长度为 512 整数倍的消息串并把消息分成长为 512位的消息块$ M_1,M_2,\ldots ,M_N$,因此填充后消息的长度为 512×N 比特。

注意到当 输入字长恰好是 448bit 时，需要填充字长 P= 512 而不是 0

2.初始化链接变量

和 MD5 类似,将 5 个 32 比特的固定数赋给 5 个 32 比特的寄存器 ABCD 和 E 作为第一次迭代的链接变量输人:

$A=0x67452301,B=0xEFCDAB89,C=0x98BADCFE,D=0x10325476,E=0xC3D2E1F0$

每一个变量给出的数值是高字节存于内存低地址，低字节存于内存高地址，即大端字节序

注意一个存储单元可以存储两位，当然也是一个字

字节序 存储内容
小端序 Buffer[4] = {0x01234567, 0x89ABCDEF, 0xFEDCBA98, 0x76543210};
大端序 Buffer[4] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476};

3.压缩函数

以 512 位的分组为单位处理消息 ,4 轮循环的模块,每轮循环由 20 个步骤组成,其逻辑如上图图 6-5 所示。每轮循环使用的步函数相同,不同轮的步函数包含不同的非线性函数(Ch、Parity、Maj、Parity)。步函数的输人除了寄存器 A、B、C、D 和 E 外,还有额外常数 $K_r(1 \leq r \leq 4)$和子消息分组(消息字)$W_t(0 \leq t \leq 79)$,t 为选代的步数，r 为轮数。

4. 循环哈希

每轮循环均以当前正在处理的 512 比特消息分组$Y_q$和 160 比特的缓存值 ABCD 和 E 为输人,然后循环更新缓存的内容。最后,寄存器 A、B、C、D、E 的当前值模 $2^{32}$加上此次迭代的输人$CV_q$，产生$CV_{q+1}$。

5.结果

得到最终散列值:全部 512 比特数据块处理完毕后,最后输出的就是 160 比特的消息摘要。

2.SHA1 的步函数

SHA1 精髓所在，即每一轮 20 个步骤中每一个步骤都在干什么

2.png

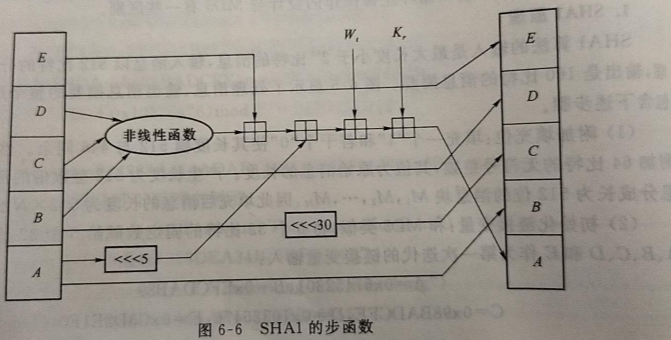
SHA1 每运行一次步函数，A、B、C、D 的值顺序赋值给(或经过一个简单左循环移位后)B、C、D、E 寄存器。同时，A、B、C、D、E 的输人值与常数和子消息块经过步函数运算后赋值给 A。

  • $A=(ROTL^5(A)+f_1(B,C,D)+E+W_t+K_r)mod2^{23}$

  • $B=A$

  • $C=ROTL^{30}(B)mod 2^{32}$

  • $D=C$

  • $E=D$

其中,t 是步数，$0\leq t \leq 79$,(因为一共 20 * 4 = 80 步)，r 为轮数,$1 \leq r \leq 4$。

图中非线性函数输人 3 个 32 比特的变量 B、C 和 D 进行操作,产生一个 32 位的输出，其定义如下:
3.png

图 6-6 中$K_r$是循环中使用的额外常数,其值定义如下。

$K_r$的 4 个取值分别为 2、3、5 和 10 的平方根，然后再乘以$2^{30} = 1073741824$,最后取乘积的整数部分。以计算 $K_4$为例，

$\sqrt{10} \approx 3.162 277 660 168 379 331 998 893 544 432 7$,

$\sqrt{10} \times 2^{32}= \sqrt{10} \times 1073 741 824 \approx 3 395469782.823647 771 064 393 520 381$,

最后取求积的整数部分得$(3395469782){10}=(CA62C1D6){16}$。

4.png

$ROTL^n(x)$表示对 32 比特的变量 x 循环左 n 比特。

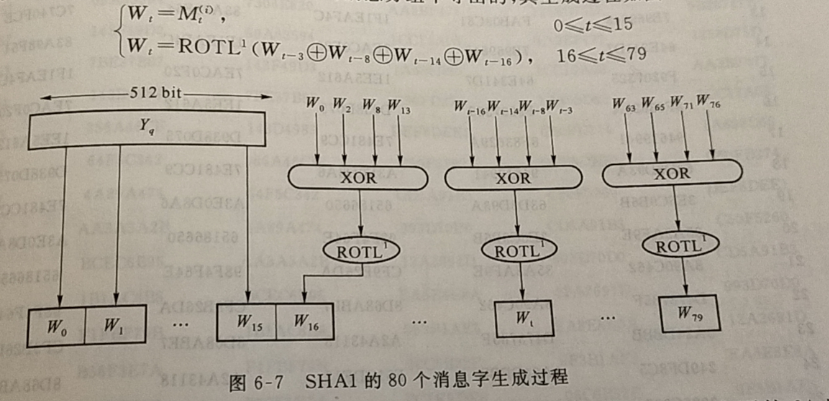
32 比特的消息字 $W_t$是从 512 比特的消息分组中导出的,其生成过程如图 6-7 所示

5.png

从图 6-7 可以看出,在前 16 步处理中 $W_t$值等于消息分组中的相应字,而余下的 64 步操作中,其值是由前面的 4 个值相互异或后再循环移位得到。上述操作增加了消息比特的扩散，故对于相同长度的消息找出另一个杂凑值相同的消息会非常困难。

3. 样例

用 SHA1 处理 ASCII 码序列“iscbupt”

解：首先将消息进行填充,填充后消息分组赋值给 16 个 32 比特的字:

$W_0=0x69736362,W_1=0x75707480,W_2=W_3=W_4=W_5=W_6=0x00000000$

$W_7=W_8=W_9=W_{10}=W_{11}=W_{12}=W_{13}=W_{14}=0x00000000,W_{15}=0x00000038$

iscbupt 的长度为 7，共 56(<64)位 bit，十六进制为$(38)_{16}$

初始散列值为:
$A=0x67452301,B=0XEFCDAB89C=0x98BADCFE,D=0x10325476,E0xC3D2E1F0$

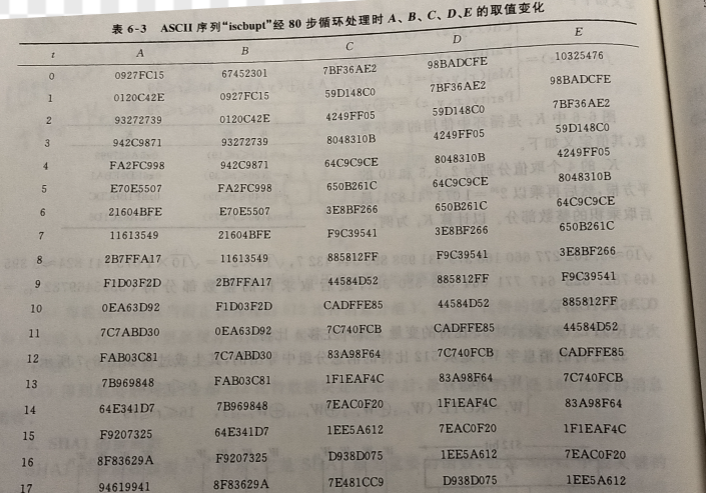
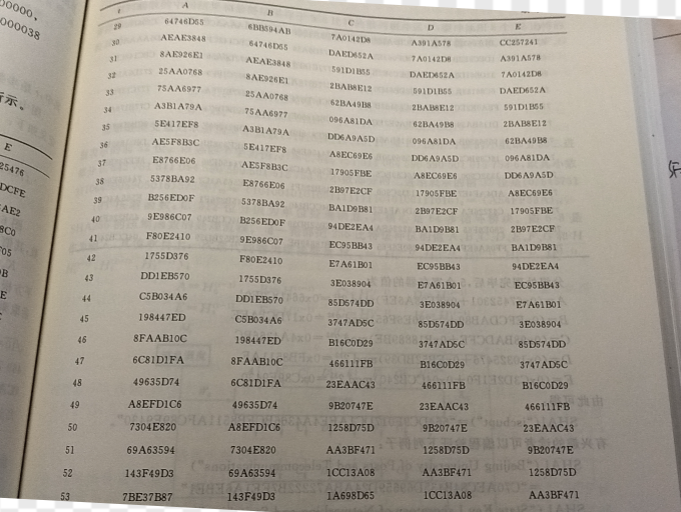
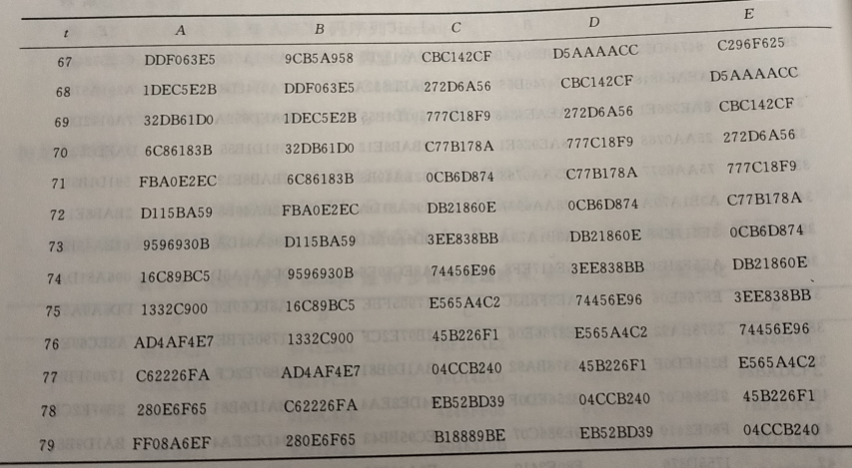
经过 80 步循环后这 5 个 32 比特的寄存器 A、B、C、D 和 E 的值如表 6-3 所示。

用手机截的图，认为不是很重要，懒得手打了，如果要验证的话前几组数据应该就够了

6.png

7.png

8.png

9.png

10.png

分组处理完毕后,5 个寄存器的值为:

$A=(0x67452301+0xFF08A6EF)mod 2^{32}=0x664DC9F0$

$B=(0xEFCDAB89+0x280E6F65)mod 2^{32}=0x17DC1AEE$

$C(0x98BADCFE+0xB18889BE)mod 2^{32}=0x4A4366BC$

$D=(0x10325476+0xEB52BD39)mod 2^{32} = 0xFB8511AF$

$E=(0xC3D2E1F0+0x04CCB240)mod2^{32}=0xC89F9430$

由此可得:

SHA1(“iscbupt”)=“664DC9F017DC1AEE4A4366BCFB8511AFC89F9430”

4.C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<iostream>
#include<vector>
#include<string>
using namespace std;

vector<int> X;//8*64=512，每个下标存放8位
int W[80];//32位为一组
int A, B, C, D, E;
int A1, B1, C1, D1, E1;//缓冲区寄存器,产生最后结果
int Turn;//加密分组数量
void printX() {//输出填充后的文本
    for (int i = 0; i < X.size(); i++) {
        printf("%02x", X[i]);
        if ((i + 1) % 4 == 0)
            printf(" ");
        if ((i + 1) % 16 == 0)
            printf("\n");
    }
}
int S(unsigned int x, int n) {//循环左移
    return x >> (32 - n) | (x << n);
}
void append(string m) {//文本的填充处理
    Turn = (m.size() + 8) / 64 + 1;
    X.resize(Turn * 64);
    int i = 0;
    for (; i < m.size(); i++) {
        X[i] = m[i];
    }
    X[i++] = 0x80;
    while (i < X.size() - 8) {
        X[i] = 0;
        i++;
    }
    long long int a = m.size() * 8;
    for (i = X.size() - 1; i >= X.size() - 8; i--) {
        X[i] = a % 256;
        a /= 256;
    }
}
void setW(vector<int> m, int n) {//W数组的生成
    n *= 64;
    for (int i = 0; i < 16; i++) {
        W[i] = (m[n + 4 * i] << 24) + (m[n + 4 * i + 1] << 16)
            + (m[n + 4 * i + 2] << 8) + m[n + 4 * i + 3];
    }
    for (int i = 16; i < 80; i++) {
        W[i] = S(W[i - 16] ^ W[i - 14] ^ W[i - 8] ^ W[i - 3], 1);
    }
}
int ft(int t) {//ft(B,C,D)函数
    if (t < 20)
        return (B & C) | ((~B) & D);
    else if (t < 40)
        return B ^ C ^ D;
    else if (t < 60)
        return (B & C) | (B & D) | (C & D);
    else
        return B ^ C ^ D;
}
int Kt(int t) {//常量K
    if (t < 20)
        return 0x5a827999;
    else if (t < 40)
        return 0x6ed9eba1;
    else if (t < 60)
        return 0x8f1bbcdc;
    else
        return 0xca62c1d6;
}
void sha1(string text) {
    A1 = A = 0x67452301;
    B1 = B = 0xefcdab89;
    C1 = C = 0x98badcfe;
    D1 = D = 0x10325476;
    E1 = E = 0xc3d2e1f0;
    append(text);
    //printX();
    for (int i = 0; i < Turn; i++) {
        setW(X, i);
        for (int t = 0; t < 80; t++) {
            int temp = E + ft(t) + S(A, 5) + W[t] + Kt(t);
            E = D;
            D = C;
            C = S(B, 30);
            B = A;
            A = temp;
        }
        A1 = A = A + A1;
        B1 = B = B + B1;
        C1 = C = C + C1;
        D1 = D = D + D1;
        E1 = E = E + E1;
    }
    printf("%08x%08x%08x%08x%08x\n\n", A1, B1, C1, D1, E1);
}

int main() {

	cout << "----------------- SHA1 -----------------\n";
	cout << "请输入要加密的明文. (如果要终止程序请按CTRL + C)\n";
    string text;
    while (true)
    {
        cin >> text;
        sha1(text);
    }
    return 0;
}

结果

1
2
3
4
----------------- SHA1 -----------------
请输入要加密的明文. (如果要终止程序请按CTRL + C)
iscbuty
c479655fcf8bb57268768a25dd4ad608bc3e36aa