Hash 函数结构

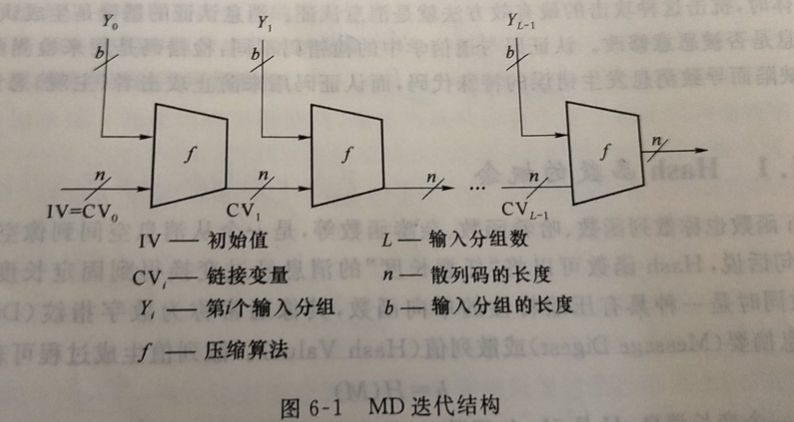
Hash 函数的一般结构如图6-1所示,称为Hash 函数迭代结构，也称为MD 结构。它由 Merkle 和 Damgard 分别独立提出,包括 MD5,SHA1 等目前所广泛使用的大多数 Hash 函数都采用这种结构。MD 结构将输人消息分为L个固定长度的分组,每一分组长为b位,最后一个分组包含输入消息的总长度,若最后一个分组不足b位时,需要将其填充为b位。由于输人包含消息的长度,所以攻击者必须找出具有相同散列值且长度相等的两条消息,或者找出两条长度不等但加入消息长度后散列值相同的消息,从而增加了攻击的难度。

1.png

迭代结构包含一个压缩函数f。压缩函数f有两个输入:一个是前一次迭代的n 位输出,称为链接变量;另一个是消息的b位分组，并产生一个 n 位的输出。因为一般来说消息分组长度b大于输出长度n,因此称之为压缩函数。第一次迭代输入的链接变量又称为初值变量,由具体算法指定,最后一次迭代的输出即为散列值。

MD5 算法

MD5 算法是美国麻省理工学院著名密码学家 Rivest 设计的,MD(Message Digest)是消息摘要的意思。Rivest 于 1992 年向 IETF 提交的 RFC1321 中对 MD5作了详尽的述 MD5 是在MD2、MD3和MD4 基础上发展而来的,尤其在 MD4 上增加了 Safety-Belts,所以MD5 又被称为是“系有安全带的 MD4”,它虽然比MD4 要稍慢一些,但更为安全。

1. MD5 算法描述

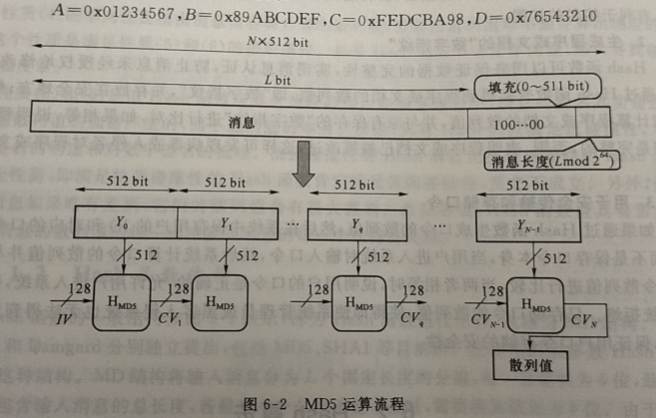
MD5算法的输人是长度小于$2^{64}$比特的消息,输出为 128 比特的消息摘要。输人消息以512 比特的分组为单位处理,其流程如下:

2.png

L为消息的长度;N 为消息扩充后分组个数:$Y_i(0 \leq i \leq N-1)$代表一个分组;IV表示初始链接变量,A、B、C、D是4个32位的寄存器;$CV_i$是链接变量,即是第i个分组处理单元的输出，也是第 i+1 个分组处理单元的输人,最后单元的输出$ CV_N$ 即是消息的散列值。

主要流程概括起来便是：消息预处理, 初始化缓冲区, 循环哈希，下面会依次介绍

2.MD5 具体流程

1. 消息预处理

  1. 附加补充位

    在长度为 K bits 的原始消息数据尾部填充长度为P bits的标识100…0，$1 \leq P \leq 512 $(即至少要填充1个bit)，使得填充后的消息位数为：$K + P \equiv 448 (mod 512).$

    注意到当 $K \equiv 448 (mod 512) $时，需要 P= 512.

  2. 附加信息

    原始消息长度（注意是长度）以 64 比特表示附加在填充结果的后面，最后得到一个长度位数为 $K + P + 64 \equiv 0 (mod 512) $的消息。

    原因: 增加攻击者伪造明文的难度. 伪造信息的长度必需要与原文长度相等(其实是同余)

    将消息长度 $Length(M)(mod2^{64})$ 以小端序的形式附加到第一步预留的 64-bit 空间中.

    后面会讲小端序和大端序

按以上步骤处理完消息之后, 将最后的得到的消息结果分割成 L 个 512-bit 分组：$Y_0, Y_1, \ldots ,Y_{L - 1}$

分组结果按 32-bit 一组, 被分为 16 组字(Word) (512 = 32 * 16)，$M_0[0],M_0[1],\ldots,M_0[15],M_1[0]\ldots, M_{L - 1}[16]$,在本文中被记作 $M_i[j]$,其中j表示字的组数.

2.初始化缓冲区

算法使用 128-bit 的缓冲区存放中间结果和最终哈希值, 128-bit 可以看做 4 组32-bit字所占的比特位(128 = 4 * 32)

被记作 $Buffer_A,Buffer_B,Buffer_C,Buffer_D$. 每个缓冲区都以小端序的方式存储数据. 将 4 块 Buffer 组合起来记为链接向量$ CV_i$

$$
CV_i=CV_{i−1}
$$

$CV_0$ 被规定为常量, 如下表格所示.(在最上面的流程图里面现实的$IV$)，即 A、B、C、D 的值分别为 0x67452301，0xEFCDAB89，0x98BADCFE，0x10325476）

每一个变量给出的数值是高字节存于内存低地址，低字节存于内存高地址，即大端字节序

注意一个存储单元可以存储两位，当然也是一个字

字节序 存储内容
小端序 Buffer[4] = {0x01234567, 0x89ABCDEF, 0xFEDCBA98, 0x76543210};
大端序 Buffer[4] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476};

3.循环哈希

调用 $H_{MD5}(M_i,CV_i)$ 函数对每组消息分组进行哈希计算.

3.png

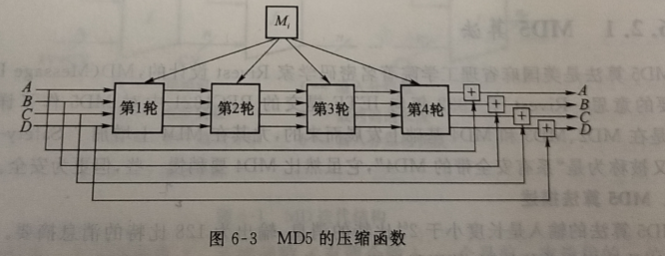
每一次$ H_{MD5}()$ 中有 4 轮结构相同的逻辑函数, 不同轮次间的唯一区别是参与计算的逻辑函数不同, 分别表示为 F、G、H、I.

下面步函数会介绍 F、G、H、I

此外, $H_{MD5}()$ 还有一个常数表 T, 常数表 T 为定义为 $T[i]=[2^{32} \times abs(sin(i))]=[4294967296 \times abs(sin(i))],1 \leq i \leq 64$ (前 32-bit 小数.) (i 是弧度),如$T[28]=[4294967296 \times abs(sin(28))] \approx [1163531501.079 3967247]$,然后其整数部分转化为十六进制$T[28]=(1163531501){10}=(455A14ED){16}$。T[i]是一个伪随机的常数,可以消除输入数据的规律性,其详细取值见表 6-1。

4.png

1
2
3
4
5
6
7
8
9
10
//常熟T[i](i = 1,...,64)
const uint32_t T[64] = {
	0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
	0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
	0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x2441453, 0xd8a1e681, 0xe7d3fbc8,
	0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
	0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
	0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x4881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
	0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
	0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391};

在本文中把 $H_{MD5}$ 的轮函数记为 $R(M_i,Buffer,T[],function_i())$. 其中, 轮函数每次调用是都会读取缓存区中的数据. 而且不同轮次之间所调用的逻辑函数也是不一样的. 此外, 每一次调用轮函数会用到不同 16 组 T 元素(对应轮函数内部的中 16 次迭代).

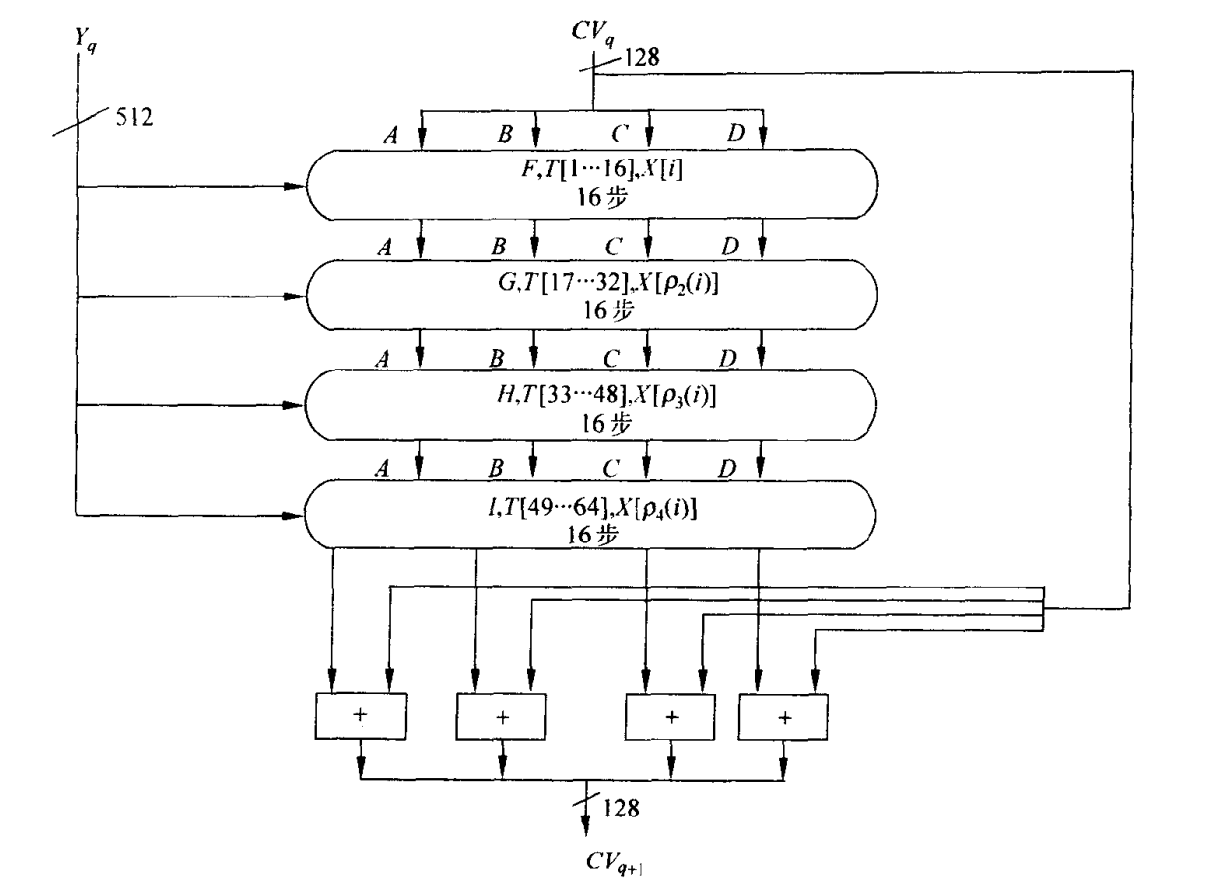
$H_{MD5}()$ 完成第四轮轮函数处理之后, 将得到的结果和输入的$ CVi$按字(每 32-bit) 分组按位加. 得到最终输出结果$ CV{i+1}$.

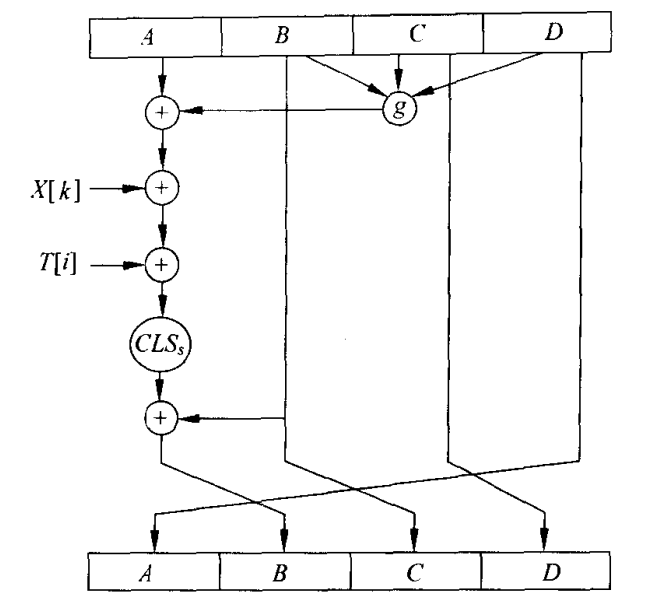
3.轮函数(压缩函数)的具体实现

MD5算法的分组处理(压缩函数)与分组密码的分组处理相似,如图 6-3 所示。它由4轮组成,512比特的消息分组M被均分为16个子分组(每个子分组为 32比特)参与每轮16步函数运算，即每轮包括16 个步骤。每步的输人是4个 32比特的链接变量和一个32比特的消息子分组,输出为32位值。经过4轮共 64 步后,得到的个存器值分别与输人链接变量进行模加，即得到此次分组处理的输出链接变量。
6.png
4 轮操作开始前,先将前一分组的链接变量(A、BC 和 D 的值)复制到另外 4 个备用记录单元AA、BB、CC和DD,以便执行最后的模加运算。

轮函数每次调用内部有 16 次迭代计算, 将轮函数当前迭代的次数记作 i

5.png

读取缓冲区中的数据, 将缓冲区按字 32-bit 分为4组, 记作 A、B、C、D

  • 第一步

    BCD 暂时不动, A 有以下 x 层计算:

    • $A+Logic_Function_{轮数}(B,C,D)$

      $F(b,c,d)=(b∧c)∨(\overline b∧d)$

      $G(b,c,d)=(b∧d)∨(c∧\overline d)$

      $H(b,c,d)=b⊕c⊕d$

      $I(b,c,d)=c⊕(b∨\overline d)$

    • $A+M_i[k]$ (k 受到当前轮数以及迭代次数 i 的影响)

    • $A+T[i]$ (受到输入影响, 与当前轮数有关)

      $ρ_1(i)=i$

      $ρ_2(i)=(1+5i)mod16$

      $ρ_3(i)=(5+3i)mod16$

      $ρ_4(i)=7imod16$

    • A 循环(注意是循环）左移 s 位 (s 由一个常量表给出)

      s[ 1…16] = { 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22 }
      s[17…32] = { 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20 }
      s[33…48] = { 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23 }
      s[49…64] = { 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21 }

    • A + B

  • 第二步

    对缓冲区中的四个字按字右循环位移 1 个字 即新的缓冲区$ Buffer′=D′||A′||B′||C′$

也就是说, 一组消息的压缩要经过这样的过程:

  1. 轮次一(F)

    1
    2
    3
    4
    5
    /* [abcd k s i] a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s). */
    [ABCD  0 7  1][DABC  1 12  2][CDAB  2 17  3][BCDA  3 22  4]
    [ABCD  4 7  5][DABC  5 12  6][CDAB  6 17  7][BCDA  7 22  8]
    [ABCD  8 7  9][DABC  9 12 10][CDAB 10 17 11][BCDA 11 22 12]
    [ABCD 12 7 13][DABC 13 12 14][CDAB 14 17 15][BCDA 15 22 16]

  2. 轮次二(G)

    1
    2
    3
    4
    5
    /* [abcd k s i] a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s). */
    [ABCD  1 5 17][DABC  6 9 18][CDAB 11 14 19][BCDA  0 20 20]
    [ABCD  5 5 21][DABC 10 9 22][CDAB 15 14 23][BCDA  4 20 24]
    [ABCD  9 5 25][DABC 14 9 26][CDAB  3 14 27][BCDA  8 20 28]
    [ABCD 13 5 29][DABC  2 9 30][CDAB  7 14 31][BCDA 12 20 32]

  3. 轮次三(H)

    1
    2
    3
    4
    5
    /* [abcd k s i] a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s). */
    [ABCD  5 4 33][DABC  8 11 34][CDAB 11 16 35][BCDA 14 23 36]
    [ABCD  1 4 37][DABC  4 11 38][CDAB  7 16 39][BCDA 10 23 40]
    [ABCD 13 4 41][DABC  0 11 42][CDAB  3 16 43][BCDA  6 23 44]
    [ABCD  9 4 45][DABC 12 11 46][CDAB 15 16 47][BCDA  2 23 48]

  4. 轮次四 (I)

    1
    2
    3
    4
    5
    /* [abcd k s i] a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s). */
    [ABCD  0 6 49][DABC  7 10 50][CDAB 14 15 51][BCDA  5 21 52]
    [ABCD 12 6 53][DABC  3 10 54][CDAB 10 15 55][BCDA  1 21 56]
    [ABCD  8 6 57][DABC 15 10 58][CDAB  6 15 59][BCDA 13 21 60]
    [ABCD  4 6 61][DABC 11 10 62][CDAB  2 15 63][BCDA  9 21 64]

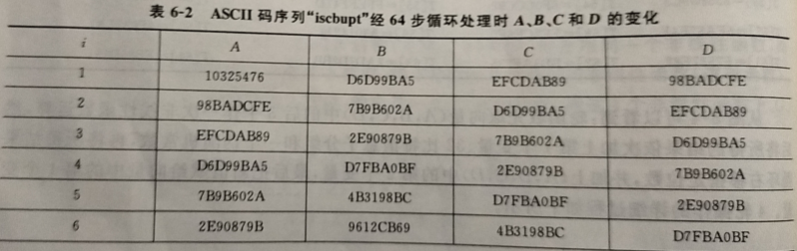
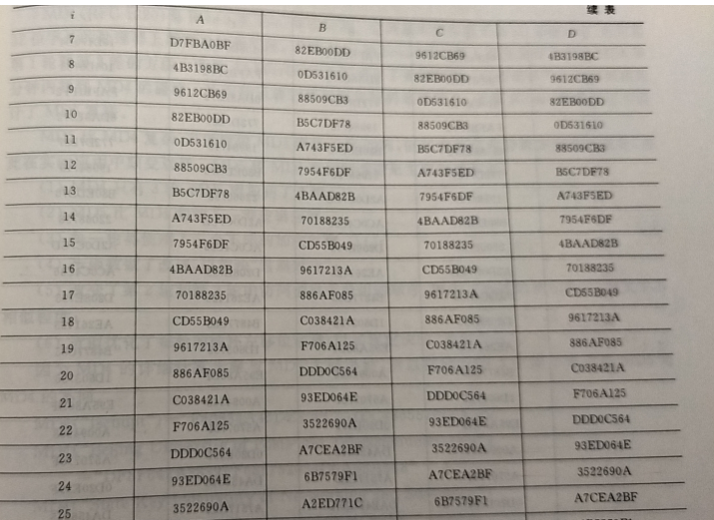
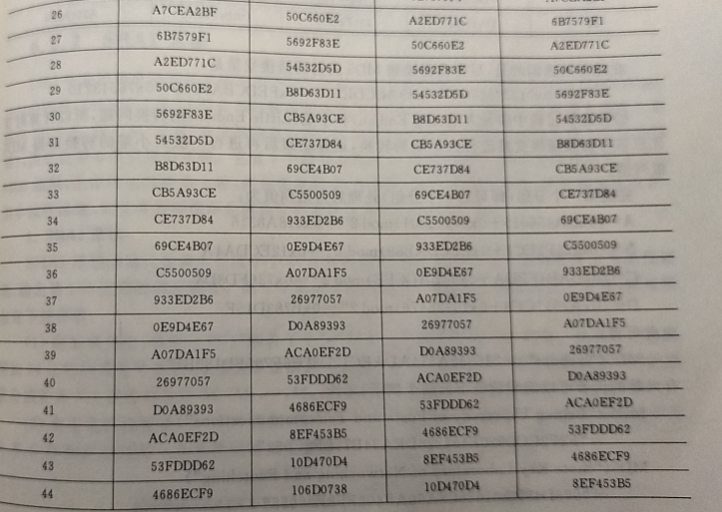
4. 案例

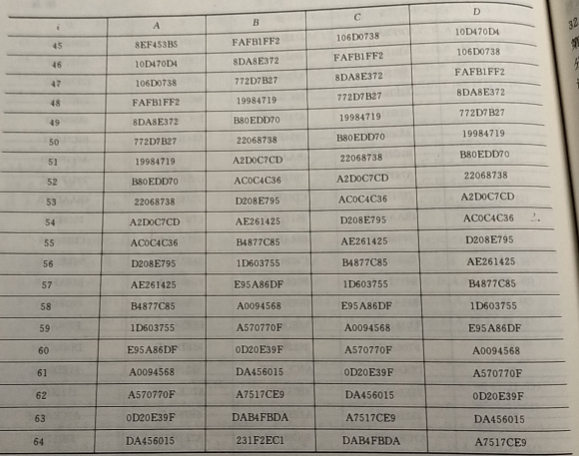
用 MD5 算法处理 ASCII 码序列“iscbupt”

我是手机拍的，懒得手打了，请见谅(❁´◡`❁)

7.png
8.png
10.png
9.png
在此特别强调的是,尽管前面提到 MD5的初始链接变量是:

A=0x01234567,B=0x89ABCDEF,C=0xFEDCBA98,D=0x76543210

但在运算过程中涉及大端(Big Endian)和小端 Little Endian)的转换问题，所以计算时首先应该将初始链接变量进行大小端的转换,运算结束后再进行一次大小端的转换即得 MD5 散列值。

完成第一个分组(即最后一个分组)处理后得散列值为:
$A=(0xDA456015+0x67452301)mod 2^{23}=0x418A8316$

$B=(0x231F2EC1+0xEFCDAB89)mod 2^{32}=0x12ECDA4A$

$C=(0xDAB4FBDA+0x98BADCFE)mod 2^{32} = 0x736FD8D8$

$D=(0xA7517CE9+0x10325476)mod2^{32}=0xB783D15F$

由此可得:
MD5(“iscbupt”)=“16838A414ADAEC12D8D86F735FD183B7”

5.代码实现

大量注释来袭 o((>ω< ))o

还有就是注意一个字就是 8bit，注意有地方看不懂是不是没换算的问题，如果还是不懂请评论留眼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
#include <iostream>
#include <string>
#include <stdint.h> // for uint* type,无符号的n位整数（unsigned n-bit integer）
#include <limits.h> // for CHAR_BIT
using namespace std;

// 默认的T
const uint32_t T[64] = {
   0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
   0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
   0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x2441453, 0xd8a1e681, 0xe7d3fbc8,
   0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
   0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
   0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x4881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
   0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
   0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391};

// 用于获取循环左移的次数
const unsigned int SHIFT[4][4]{
   {7, 12, 17, 22},
   {5, 9, 14, 20},
   {4, 11, 16, 23},
   {6, 10, 15, 21}};

// 填充位，0x80是一个十六进制数，表示一个二进制数10000000
//是因为填充的bit需要是一个1和若干个0
const uint8_t PADDING[] = {
   0x80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
   0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
   0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
   0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};

// 用于循环左移
inline uint32_t Left_Rotate32(uint32_t x, unsigned int num)
{
   num &= 31;
   return (x << num) | (x >> (-num & 31));
}

// 非线性函数FGHI
inline uint32_t Logic_Function(int Round_i, uint32_t b, uint32_t c, uint32_t d)
{
   switch (Round_i)
   {
   case 3:
   	return c ^ (b | ~d);
   case 2:
   	return b ^ c ^ d;
   case 1:
   	return (b & d) | (c & ~d);
   case 0:
   	return (b & c) | (~b & d);
   }
   return 0;
}

//获取T[i]中的i (受到输入影响, 与当前轮数有关)
inline unsigned int Substituion(int Round_i, int i)
{
   switch (Round_i)
   {
   case 0:
   	return i;
   case 1:
   	return (1 + 5 * i) % 16;
   case 2:
   	return (5 + 3 * i) % 16;
   case 3:
   	return (7 * i) % 16;
   }
   return 0;
}

// 参数是第i轮，ABCD，和消息分组M
void Round_Function(int Round_i, uint32_t buffer[4], const uint32_t message_block[16])
{
   //每轮需要进行16个步骤
   for (int i = 0; i < 16; i++)
   {
       // 1.步函数执行
   	// A + +Logic_Function_{轮数}(B,C,D)
   	buffer[0] += Logic_Function(Round_i, buffer[1], buffer[2], buffer[3]);
   	// A+M_i[k] (k 受到当前轮数以及迭代次数 i 的影响)
   	buffer[0] += message_block[Substituion(Round_i, i)];
   	// A+T[i] (受到输入影响, 与当前轮数有关)
   	buffer[0] += T[Round_i * 16 + i];
   	// A 循环左移 s 位 (s 由一个常量表给出)
   	buffer[0] = Left_Rotate32(buffer[0], SHIFT[Round_i][i % 4]);
   	// 最后A + B
   	buffer[0] += buffer[1];

   	// 2. 对缓冲区中的四个字按字右循环位移 1 个字
   	// Buffer′=D′||A′||B′||C′
   	uint32_t bufferCache = buffer[3];
   	buffer[3] = buffer[2];
   	buffer[2] = buffer[1];
   	buffer[1] = buffer[0];
   	buffer[0] = bufferCache;
   }
   return;
}

//chain_vector即ABCD，消息分组message_block有16个子分组，每个子分组位32bit
void Hash_MD5(uint32_t chain_vector[4], const uint32_t message_block[16])
{
   // 将chain_vector赋给buffer，buffer作为中间tmp
   uint32_t buffer[4];
   memcpy(buffer, chain_vector, 128 / CHAR_BIT);

   // 进行四轮迭代
   for (int i = 0; i < 4; i++)
   	Round_Function(i, buffer, message_block);

   // 将得到的结果和输入的CV_i按字(每 32-bit) 分组按位加. 得到最终输出结果CV_{i+1}.

   for (int i = 0; i < 4; i++)
   	chain_vector[i] += buffer[i];
}

__uint128_t MD5(string _message)
{
   /*
   //  1.预处理的消息
   //  填充和追加长度信息
   //  填充缓存数组
   //  附加messageBITcount，在c++中自然以尾序存储
   */

   // 获取信息的长度,_message是还未处理的信息
   uint64_t messageLength = _message.length();
   // 将信息的字节长度转换为位（bit）长度，CHAR_BIT通常指的是8
   uint64_t messageBitCount = messageLength * CHAR_BIT;

   //计算需要多少个512位的块来存储信息
   //这里先将messageBitCount加上64，是因为后面需要填充原始消息开头的低64位
   //+1是为了C++默认向下取整，我们需要向上取整
   int blockCount = (messageBitCount + 64 - 1) / 512 + 1;
   //数组的大小是64 * blockCount，这样可以使信息的长度恰好是blockCount个512位的块的倍数。
   uint8_t message[64 * blockCount];
   memcpy(message, _message.c_str(), messageLength);
   //在信息的末尾填充特定的填充字符，直到信息长度达到64的倍数,for语句中-8是为了填充原始消息开头的低64位
   for (int i = messageLength, j = 0; i < (64 * blockCount - 8); i++)
   	message[i] = PADDING[j++];
   //在最后空缺的64位上填充  以64比特表示的原始消息长度
   //实际上是将messageBitCount的低64位添加到了message + (64 * blockCount - 8)后面
   memcpy(message + (64 * blockCount - 8), &messageBitCount, 64 / CHAR_BIT);

   // 构建对象M，每一个M有16个子分组，每个子分组位32bit
   uint32_t *messageBuffer = new uint32_t[16];

   /*
   //  2.初始化CV
   //  注意CV1 的ABCD位大端序
   */
   uint32_t res[4] = {0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476};
   for (int i = 0; i < blockCount; i++)
   {
   	// 更新 Message_Block，即M0，M1，M2。。。
   	memcpy(messageBuffer, message + 64 * i, 64);
   	//对每一个M进行hash压缩函数
   	Hash_MD5(res, messageBuffer);
   }

   /*
   //  3.将最后得到的ABCD即res返回md5
   */
   __uint128_t md5 = 0;
   for (int i = 0; i < 4; i++)
   		md5 += (__uint128_t)res[i] << (i * 32);

       //释放动态分配的内存
       //当你使用 new 关键字动态地分配内存时，在不再使用那块内存后使用 delete[] 来释放它
       //不释放动态分配的内存，那么程序可能会消耗掉所有的可用内存，导致所谓的内存泄漏
   	delete[] messageBuffer;
   	return md5;
}

void MD5_Print(__uint128_t in)//将128位整数的每一个字节以十六进制形式打印出来。
{
   //__uint128_t 是128位，但 printf 函数只能按字节（即8位）来处理数据。
   //所以，我们需要利用unsigned char逐个访问128位的整数按字节并拆分，然后逐个字节地打印。
   unsigned char *ptr = (unsigned char *)&in;
   for (int i = 0; i < 16; i++)
       //%02x 是一个格式说明符，它将以两位十六进制格式打印一个字节，并在需要时在前面补零。
   	printf("%02x", ptr[i]);
}

int main(void)
{
   cout << "----------------- MD5 -----------------\n";
   cout << "请输入要加密的明文. (如果要终止程序请按CTRL + C)\n";
   string str;
   cout << "text: ";
   getline(cin, str);
   //__uint128_t一个无符号的128位整数,可存储的值（2^128 - 1）
   __uint128_t md5 = MD5(str);

   cout << "result: ";
   // 注意这个md5类型是__uint128_t，我们需要的是能将这个整数以16进制输出
   MD5_Print(md5);

   return 0;
}

结果

1
2
3
4
----------------- MD5 -----------------
请输入要加密的明文. (如果要终止程序请按CTRL + C)
text: iscbupt
result: 16838a414adaec12d8d86f735fd183b7